Option vega

Option vega, represented by Greek symbol ν (nu), is a mathematical tool used to capture the responsiveness of option value to changes in the volatility of option's underlying asset's value. In other words, option vega is option's sensitivity to fluctuations in the underlying asset price.

What does option vega say?

Option is a financial contract which gives one party the option to buy or sell the underlying asset while the other party has obligation to honor the contract. The contract can be sold before its expiration, and it is possible to calculate its value. The value of the contract depends on many factors, for example the price of the underlying asset (option delta & option gamma), interest rates, time (option theta), volatility, and other factors.

If the volatility of the prices of the underlying asset changes, then the option vega changes as well.

What values can option vega take?

Option vega grows as the option comes from being out-the-money closer to being at-the-money, and then it declines as the option starts being deeply in-the-money. Option vega is greatest for options at-the-money. Option vega is smaller for options completely out-the-money or very much valuable.

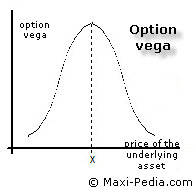
This can be explained more easily by saying that if the option is worthless, it does not matter much how volatile the underlying asset is because the chance that the option suddenly flips into in-the-money is relatively small. If the option is deep in the money, the chance that the option suddenly becomes worthless with increased volatility is also relatively slim. But, if the option is at-the-money, that is on the verge of being worthless or valuable, then even a relatively small change in the volatility in the price of the underlying asset can change the position.

You can notice that option vega takes values similar to option gamma.

Option vega implications

There are several important rules related to option vega.

• Option vega is similar for call and put options.
• Options with short time to expiration have lower option vega than long time before expiration. This is so because long-term options are exposed to a greater risk of ending out of the money then options with only a few days to expiration. The price of the underlying asset is more likely to go 50% up or down in long term than in short term.
• Options are most sensitive to changes in the volatility of the underlying asset when they are at-the-money.
• Options out-the-money and in-the-money are not affected by volatility in the prices of the underlying assets.
• Option vega can be hedged with another option only.

How can I calculate option vega?

Option vega is a measure of option's sensitivity to the volatility of the underlying asset. Mathematically, option vega is first derivation of the option's value function by volatility. Schematically, we can express this using the following formula:

,

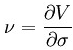where dV is the value of option and dσ is volatility. We can expand this equation using the Black-Scholes model into the following exact mathematical formula:

,

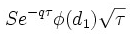The d1 parameter can be expressed as follows:

.

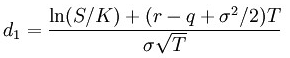Phi represents the cumulative distribution function of standard Normal distribution, r is risk-free interest rate (for example U. S. Government Treasury 30-day rate), q is the dividend yield, σ is volatility, T is time to expiration, S is the price of the underlying asset, and K is the strike price.

What is the relationship between option vega and implied volatility?

Option vega is the highest when the option is at-the-money.

Implied volatility is the lowest when the option is at-the-money.