Black-Scholes model

The Black-Scholes model is a tool for pricing equity options. The Black-Scholes model, often also called using its full name Black-Scholes Option Pricing Model, is an approach for calculating the value of a stock option, let it be a call option or a put option.

The basic idea behind the Black-Scholes model is that the price of an option is determined implicitly by the price of the underlying stock.

How does the Black-Scholes model work?

The Black-Scholes model is a mathematical model based on the notion that prices of stock follow a stochastic process, in other words the price of a stock in time t+1 is independent from the price in time t. This is also referred to as random walk.

Assuming that stock prices follow random walk, it already suggests that we will need to involve some math and statistics. The Black-Scholes model is a formula that can be expressed as described in the following paragraph.

What is the Black-Scholes formula?

The Black-Scholes model is basically a formula that is used to calculate option values. The Black-Scholes formula consists of three parts. The main equation and two formulas for calculating parameters.

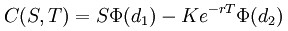
This part of the Black-Scholes formula tells us that the price of a European-style call option with expiration date in time T written on stock S is equal to the price of the stock adjusted for volatility, interest rate, and spread minus present value of the stock delivery price (or a strike price) also adjusted for volatility, interest rate, and spread.

The parameters d1 and d2 in the Black-Scholes formula can be calculated the following way:

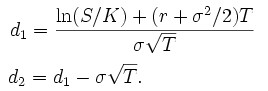
The d1 and d2 are parameters to the φ phi in the first equation. Phi represents a cumulative distribution function of Normal distribution. In layman terms, we calculate the parameters d1 and d2 and look up a corresponding tabularized value in a book, and then we plug those values back into the first formula.

The Black-Scholes formula for a European-style put option is very similar to the Black-Scholes formula for a call option. It is the following:

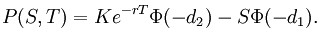
This Black-Scholes formula tells us that a value of a put option can be calculated as a present value of the stock delivery price minus the price of the stock, both adjusted for volatility, interest rate, and spread.

Black-Scholes formula calculation example

The Black-Scholes formula is used to calculate the value of an option. We can demonstrate the working of the Black-Scholes formula on an example.

Let us assume that the current price of shares of company XYZ is $100 and you would like to get an option to purchase one share of XYZ company stock for $95. The option expires in three months. We also assume that the stock pays no dividends. The standard deviation of the stock’s returns is 50% per year, and the risk-free rate is 10% per year, we can calculate the value of the option as follows:

d1 = [ln($100/$95) + (0.10 + 0.25/2) * 0.25]/ 0.50 * √0.25 = 0.43
d2 = 0.43 - 0.50 * √0.25 = 0.18
N(0.43) = 0.6664
N(0.18) = 0.5714

Plugging these parameters into the formula, we get:

C(S,T) = $100 * 0.6664 - $95 * e ^{-(0.10 * 0.25)} * 0.5714 = 66.64 - 52.94 = $13.70

You can go to our Black-Scholes formula option value on-line calculator page to run some calculations and verify this result.

Note, this Black-Scholes formula example is used to value a call option. The Black-Scholes model can also be used to price puts options. If you want to value a put option, you can either calculate it from scratch, similar to what we did above but just using the P(S,T) formula, or recalculate the Black-Scholes model through the put-call parity. Using the put-call parity approach to calculate put option value given that you know the call option value, you would solve the put-call parity equation for the value of the put option. See the following example:

P(S,T) = C(S,T) + B(T) - S(T) = C(S,T) + X * e^-rT - S(T) = $13.70 + $95 * e^{-(0.10 * 0.25)} - $100 = $6.35

Ready to know what are the limitations of these results?

What are the assumptions behind the Black-Scholes model?

Understanding the Black-Scholes model assumptions is very important for the application of the model to real-world scenarios. Listing of the Black-Scholes model assumptions is provided on the next page: Black-Scholes model assumptions.

What is the history of the Black-Scholes model?

The Black-Scholes model was developed by Fischer Black and Myron Scholes in 1973. Robert Merton also participated in the model’s creation; hence that is why the model is sometimes referred to as the Black-Scholes-Merton model. Black, Sholes, and Merton were awarded the Nobel Prize in Economics for the Black-Scholes model. All three men were college professors working at both the University of Chicago and MIT at the time.

Does the Black-Scholes model work in the real world?

There are known restrictions of the Black-Scholes model when using it in the real world. The major problem is that capital markets often move in ways not consistent with the random walk hypothesis. This also relates to the assumption of the constant volatility. Volatility is not constant in real world. Very short-term options can be valued using the basic Black-Scholes formula because volatility can change only so much in only a few days, but invalidation of these assumptions in longer term in the real world makes the Black-Scholes formula not work for mid-term and long-term options.

The Black-Scholes model was later improved to deal with some limitations of the real world. For example the Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) model replaces the constant volatility with stochastic, or random, volatility.

Are there any models that are more advanced than Black-Scholes?

The Black-Scholes model is subject to many limitations and assumptions as discussed on the Black-Scholes assumptions page. Every model is only an approximation of the real world, and every model has some limitations. The Black-Scholes model was revolutionary in a way it approached options valuation.

Throughout the years, many other models emerged trying to provide more accurate approach to option valuation. However, with a little generalization, we can say that probably most of them are enhancements of Black-Scholes. All of them are based on the same valuation principle. The difference between models is mostly how they address assumptions of the Black-Scholes model. We already mentioned that for example the GARCH model substitutes constant volatility with a stochastic one. Other models address other assumptions, for example the assumption of constant interest rate, or address them differently. We can name a few models related to valuations, for example: Garman-Kolhagen Option Pricing Model which is used for currency options, Hull-White, Cox-Ingersoll-Ross, Vasicek, Cox-Ross-Rubenstein model, etc.