Option gamma

Option gamma, often expressed using the Greek letter Γ, is a mathematical tool used in the option theory to explain the relationship between the value of an option and the price of the underlying asset. Option gamma is the option's sensitivity to change in the sensitivity of the option value to changes in the underlying asset price.

An option is a contract between two parties, between a buyer and seller, where one party has the right to purchase the underlying asset (call option) or to sell the underlying asset (put option) while the other party has the obligation to honor the contract. The other party is compensated for the obligation by so-called option premium which reflects the option's intrinsic value. The price of the option is determined by the price of the underlying asset, and the relationship between the price of the underlying asset and the option value is given by many parameters. Option gamma tells us how the option price responds to changes in the underlying asset price changes.

Option gamma explained

Option gamma can be better explained using pictures. Option gamma measures the curvature of the option price function curve. Option gamma can also be described as the "speed" at which the value of an option changes with changes in the price of the underlying asset.

Option gamma changes as the underlying asset price changes.

• Option gamma is highest for options at-the-money. Any change, even a small one, in the price of the underlying asset affects the value of the option significantly. This is the point at the top of the curve on the picture below.
• Gamma is lowest when an option is deeply in-the-money or completely out-the-money. Any change in the price of the underlying asset has little or no effect on the option value.

You can see this on the following graph:

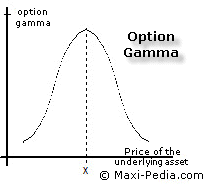
As the price of the underlying asset grows, so grows option gamma. But only to a certain point where it starts declining.

Option gamma example - What does option gamma tell me?

Option gamma measures the sensitivity of an option to the change in the price of the underlying asset. We can demonstrate this on the following two examples.

Example 1

When the price of the underlying asset changes by 1% (note, 1% not 1 dollar), the value of an out-of-money option changes by, let's say, 0.2%. In the next step, the price of the underlying asset changes by another 1%. Now, the value of the option changes by more than before, this time it changes by 0.25%.

The option delta changes by 0.05. 0.05 is the option gamma.

Example 2

Let's say the price of the underlying asset changes by 1%. The value of an at-the-money option changes by 0.5%. Now, the underlying stock price changes by another 1% which leads to a 0.6% change in the value of the option. The change in option delta, that is the option gamma, is 0.1.

How does option gamma compare to option delta?

Option gamma is one step above option delta. Option delta measures the slope of the price curve. The option gamma measures the curvature of the price curve.

Option gamma implications

Let us summarize a number of very important option gamma implications.

• Options at-the-money have the highest gamma.
• Short option positions are characterized by negative option gamma. This applies to both call and put options.
• Gamma is the same for call and put options.
• Options with short term to expiration have higher option gamma then long-term options. In other words, short-term options are more sensitive.
• Option gamma increases as the option approaches its maturity.
• When option gamma is high, option delta changes rapidly. When option gamma is small, option delta changes relatively little.
• Futures have gamma constant and equal to zero.

Ready to get into some math?

How do we calculate option gamma?

As we said already, option gamma measures the sensitivity of an option to changes in the prices of the underlying asset. Mathematically, option gamma is second derivation of the option price (value) function. We can express this schematically using the following formula:

,

where the d²V is the value of the option and dS² is the price of the underlying asset. The schematic notation above can be expanded into the following concrete mathematical formula derived from the Black-Scholes model formula:

,

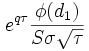where

,

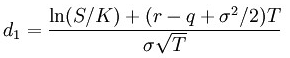where φ (phi) represents the cumulative distribution function of standard Normal distribution, r is risk-free interest rate (for example U. S. Government Treasury 30-day rate), q is the dividend yield, σ is volatility, T is time to expiration, S is the price of the underlying asset, and K is the strike price.

Are there any other factors related to option value?

Yes, option gamma and option delta are the two most commonly analyzed characteristics related to option's sensitivity to changes in the underlying asset price. Besides option gamma and option delta, we also measure sensitivities to other factors, such as volatility (option vega), interest rates, time (option theta), and others. These sensitivity measures are collectively called "the Greeks" because they are represented by the Greek letters (delta, gamma, rho, theta, and others).

Greeks measure option's sensitivity which in turn translates into the risk of your option position; therefore, they are very important tool in risk management. Choosing the right mix of options and other assets in your portfolio, it is possible to alter the overall risk profile of your portfolio. Sensitivity parameters derived from the Black-Scholes model are very popular among financial professionals for their ease of calculation.