Option theta

Option theta is one of the sensitivity parameters used in option theory to measure responsiveness of an option to change in time. Option theta is often represented by Greek symbol Θ. Option theta belongs to a group of option sensitivity parameters together called "Greeks".

Option theta explained

Option theta is a mathematical tool used to capture how the price or a value of an option reacts to time, specifically how it changes as the option approaches its expiration or maturity date. Option theta is also often called time decay which means exactly what it says.

An option has some value right at the moment when it is written. It has some value just because it exists and because it theoretically ties up some of the writer's money (for which the writer has to be compensated). This is called time value of an option. As the option approaches its expiration date, the option time value decreases, or we can say it "decays." However, the time value does not diminish linearly. The rate at which an option looses its value changes as the option nears its end. And the option theta sensitivity measure is the tool that is used to measure this.

What values can option theta take?

We can explain option theta using the two pictures below.

Option theta and asset price...

Option theta can be quite confusing, but it helps to think about it in plain logic. Option theta is negative because the relationship between option's value and the time to expiration is inverse. As the option ages, the time value decreases.

When thinking about the size of the option theta, it is however easier to think in terms of option theta absolute value. Option theta is the lowest (or the highest when looking at its absolute value) when an option is at-the-money. When an option is completely worthless or very valuable, then the absolute value of the option theta is minimal.

Let's use a call option as an example. A call option theta would be on the left hand side of the graph below. The current underlying asset price S would be much smaller than the exercise price X. In such case, when you have a call option that is already completely worthless, then it is worthless and not even the fact that it is far away from its expiration date helps it much. When you have a call option that is deeply in the money, then it already is in-the-money, and just mere ageing of the option does not hurt it as much as it would hurt an option that is on the verge of being in- or out-the-money.

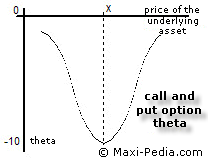
This relationship is in a way similar to two other option sensitivity indicators. Compare option theta to option gamma and option vega.

Option theta and option expiration time...

Option theta gets affected not only by whether the option is in or out of the money, but also as the option itself ages. As the option gets closer to its expiration date, it tends to loose its time value more quickly. Having 90 days to the expiration date, an option changes its value (assuming other factors are constant) from the 90th day to the 89th day only minimally. However, the same option will loose a lot of its time value between the 3rd and 2nd day before its expiration.

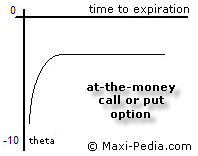
Option theta is negative and its absolute value increases as the option nears its expiration.

What are the important option theta characteristics?

The list below summarizes some important facts related to option theta.

• Option theta is a function of time and value of the underlying asset.
• The time value of either a call or put option decreases as the option approaches its expiration.
• Theta is the same for call and put options.
• Option theta is minimal (or maximal when looking at its absolute value) when an option is at-the-money.
• Option theta - its absolute value - increases as the option approaches its expiration.
• Option theta is usually negative. European put option in-the-money is an exception to the rule. Such an option can have a positive theta.

Now let's take a look how option theta is calculated.

How can I calculate option theta?

Option theta is mathematically first derivation of option's value function by time. We can express this schematically using the following equation:

,

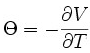where dV is the value of an option and dT is the time to expiration. Using the math of the Black-Scholes model, we can calculate the theta of an option as follows:

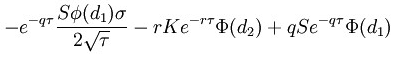 (CALL OPTION),

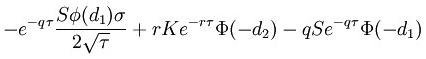 (PUT OPTION)

The d1 and d2 parameters are calculated using the following formula:

,

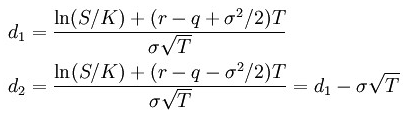where φ (phi) represents the cumulative distribution function of standard Normal distribution, r is risk-free interest rate (for example U. S. Government Treasury 30-day rate), q is the dividend yield, σ is volatility, T is time to expiration, S is the price of the underlying asset, and K is the strike price.

Are there any other option sensitivity measures I should know about?

Options are sensitive not only to the flow of time but to a number of other factors as well. Option delta and option gamma measure option sensitivity to changes in the price of the underlying asset. Option vega measures option sensitivity to the volatility of the price of the underlying asset.